7日目は電気設計を担当しております早川が、ミニ四駆のモーターをPID制御する回路を趣味で作ってみたのでその技術について解説したいと思います。
こちらの動画を御覧ください。
本来無負荷であれば14900rpmもの回転数で回るミニ四駆のモーターを、うまく制御するとここまでゆっくりヌルヌル動かせるんです。
本稿では、LTspiceという回路シミュレーターを使っての事前検討と実際の回路制作について、解説していきたいと思います。
#モーター単体のシミュレーション
まずはモーター単体のシミュレーションを考えてみます。今回はミニ四駆のレブチューン2というモーターを例に解説します。
DCモーターの等価回路として下図のようなものを見たことのある方も多いのではないでしょうか。
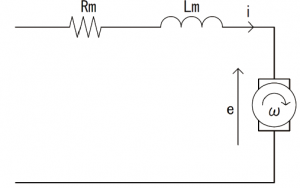
せっかく回路図で表現されたモデルがあるのですからそのままLTspiceに入力していきましょう。
今回モーターは電流駆動したいので、電圧制御電流源を使って定電流駆動します。
(電圧制御ではない電流源を使ってもできますが、次のステップでこちらが便利です)
電圧制御電流源のプロパティを開き、valueの欄でに1と入力します。(電圧と同じ値の電流を出力するようになります)
上の図でeとなっているのはモーターの誘起電圧を意味していて、回転数に比例した電圧源と考えます。
その比例定数を誘起電圧定数といい、今回はkeと表します。
回転数をωとすると
e = ke * ω
となります。
このような数式で表される電圧をLTspice上で扱う際はビヘイビア電源を使います。
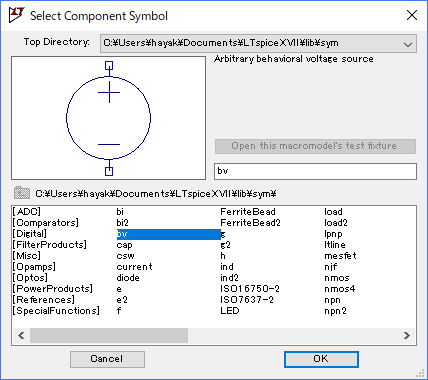
ビヘイビア電源のプロパティを開き、valueの欄に
V=V(omega)*ke
と入力します。
ωなどのギリシャ文字は変数として使えないのでLTspice上ではomegaなどと表現しましょう。
keの具体的な数値を入力しないとシミュレーションできないので、spice directiveポタンを押して次のように入力します。
以降で使う定数も全てここで入力していまいましょう。
.param ke=0.00103618021 kt=0.00103618021 Lm=145u Rm=0.4 J=7.0531e-07 D=3.8332e-07
なお、この値は私が実測したものですがかなりラフな測定方法ですので誤差が大きいと思います。値の流用の際には注意してください。
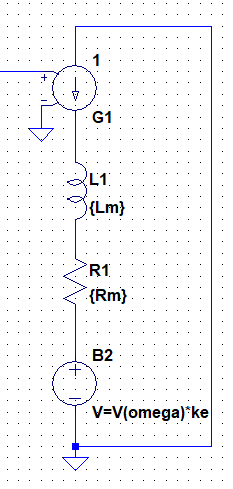
これでDCモーターの等価回路がLTspiceに入力できました。
DCモーターを電流を入力したらトルクを出力するデバイスと考えた場合、この回路の出力はktをトルク定数、流れる電流をIとすると、kt*Iとなります。
トルク定数ktと誘起電圧定数keは理論的に同じ値になります。
図の等価回路にはトルク出力のポートがありませんから、これを追加してみましょう。
ビヘイビア電源を使って
V=I(R1)*kt
と入力します。
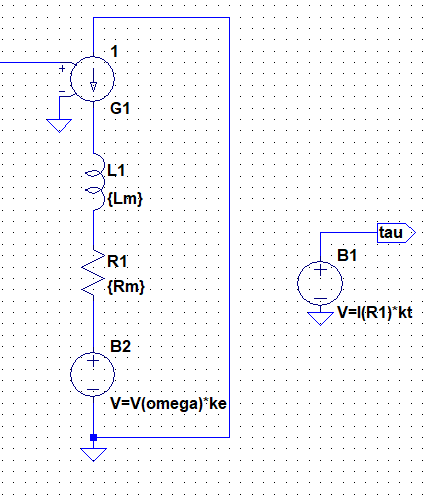
トルクtauが出力された結果、ローターが回転します。
回転数をomegaとすると、tauからomegaまでの伝達関数はローターに接続された機械系によって決まります。
モーターを無負荷で回転させることを考えると、その機械系はローターの慣性モーメントJと粘性摩擦Dによって決まる一次遅れ系とみなすことができます。
実際にはもっと複雑なのですが、正確なモデルを作ることが目的ではないですし、制御の教科書ではよくこのようにモデル化するので、それに習うことにしましょう。
tauからomegaまでの伝達関数は
1 / ( Js + D )
となります。
このようなラプラス変換された伝達関数を扱う際は電圧制御電源を使います。
valueの欄に
Laplace = 1/(J*s+D)
と入力します。
すると、入力信号に対してこの伝達関数を適用した出力が得られます。
これでモーター単体でのシミュレーションでできるようになりました。
ステップ入力に対する応答をシミュレーションと実物で比較してみましょう。
なお、入力信号としてはデータロガーで実測した、実験時の電流波形を使用しています。
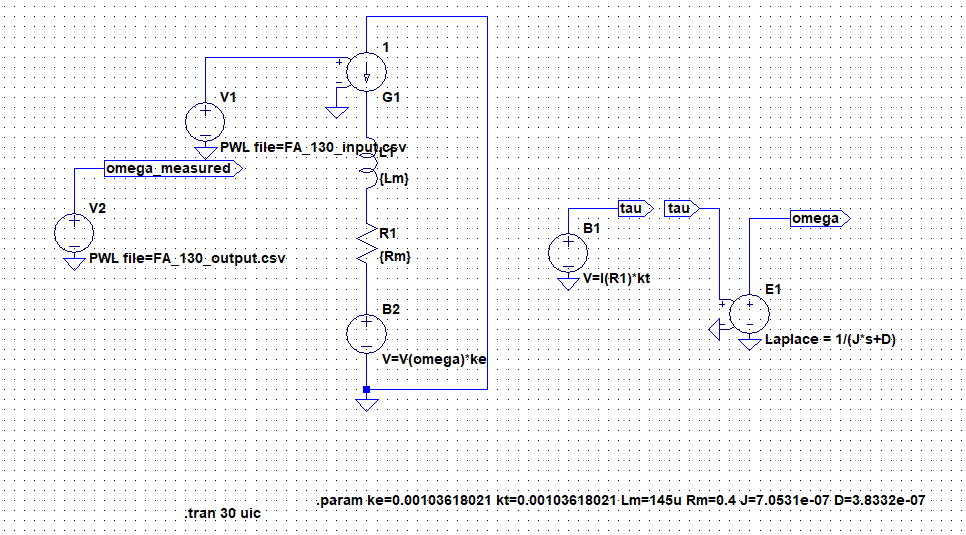
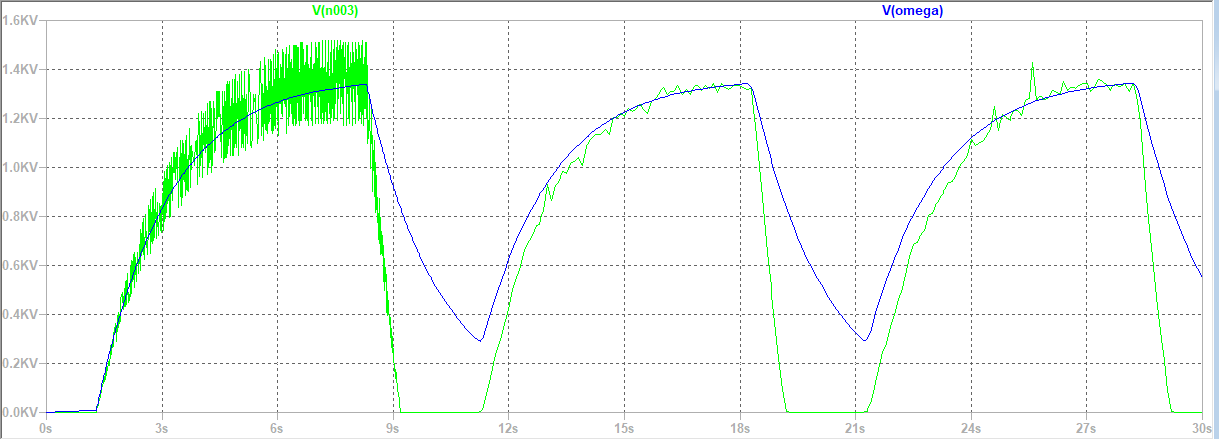
青が等価回路のシミュレーション結果、緑が実験した際の実測値です。
実測値とシミュレーション結果にズレがありますが、細かいことは気にしないで進めていきましょう。
単位が[kV]となっていますが、実際の物理量は回転数ですので、[k・rad/s]と読み換えます。
シミュレーションファイルはこちら
fa_130_step
fa_130_step
#モーターの速度制御
次はこのモーターの速度制御を考えていきましょう。
モーターの出力軸にもう一つ同じモーターを接続してそれを速度センサーとして使う系を考えてみます。
制御方式はPI制御としましょう。(PID制御に興味がある方、最後の方でPID制御も試しますので読んでいただけると!)
速度指令としては、さらにもう一つ同じモーターを用意してそれを手などで回したときの速度が指令となるような系を考えていきます。
ブロック線図で表すと次のようになります。
※「系」という日本語に馴染みがない方も多いかもしれません。英語の”system”に対応する言葉で、「仕組み」のニュアンスです。
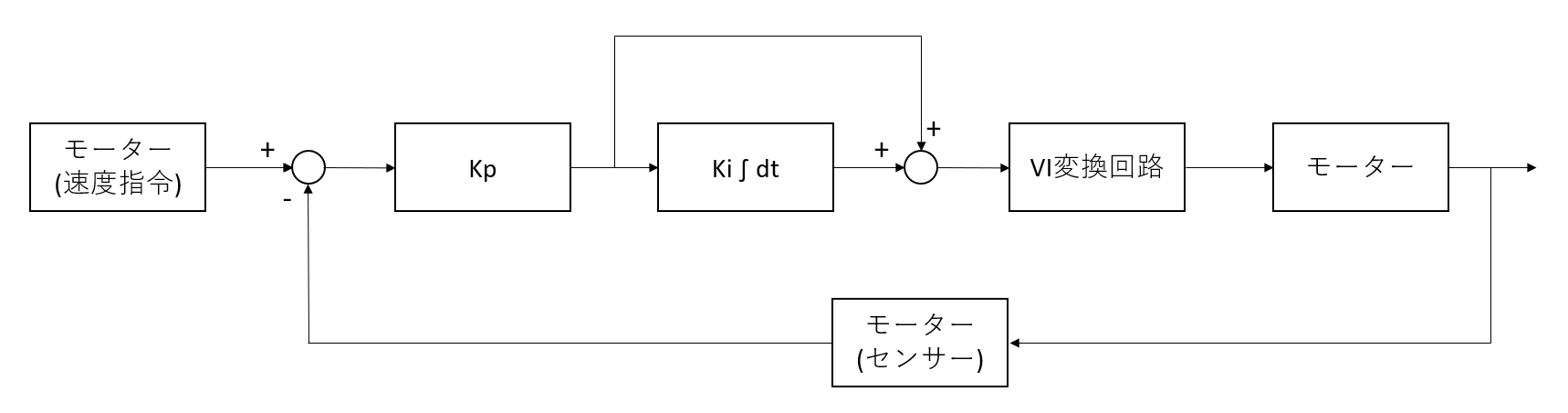
これをLTspiceでシミュレーションしていきたいと思います。
最初は実際の電子部品は使わずブロック線図を忠実にシミュレーションすることを考えます。
まず速度指令用のモーターですが、速度指令omega_targetを入力するとomega_target*keの電圧が得られる素子なので、ビヘイビア電源を使って
V=V(omega_target)*ke
で表現します。
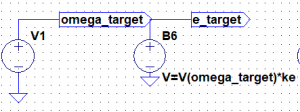
偏差の検出も同様にビヘイビア電源を使って
V=V(e_taeget)-V(sens)
と表現します。
sensは速度センサーの出力です。

これの出力をErrorとすると、PI制御器は
V=Kp*V(error) + Ki*idt(V(error),0)
となります。
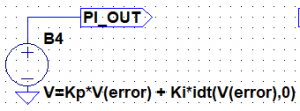
idt()は積分を行う関数です。第二引数は初期値を意味しています。
これの出力をPI_OUTとし、モーターを電流駆動したいので電圧制御電流源に渡します。
Kp,Kiの値はとりあえず1としておきます。
spice directiveボタンを押して
.param kp=1 ki=1
と入力しましょう。
速度センサーからの出力は
V=ke*V(omega)
とします。
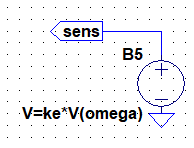
全体としては次のようになります。
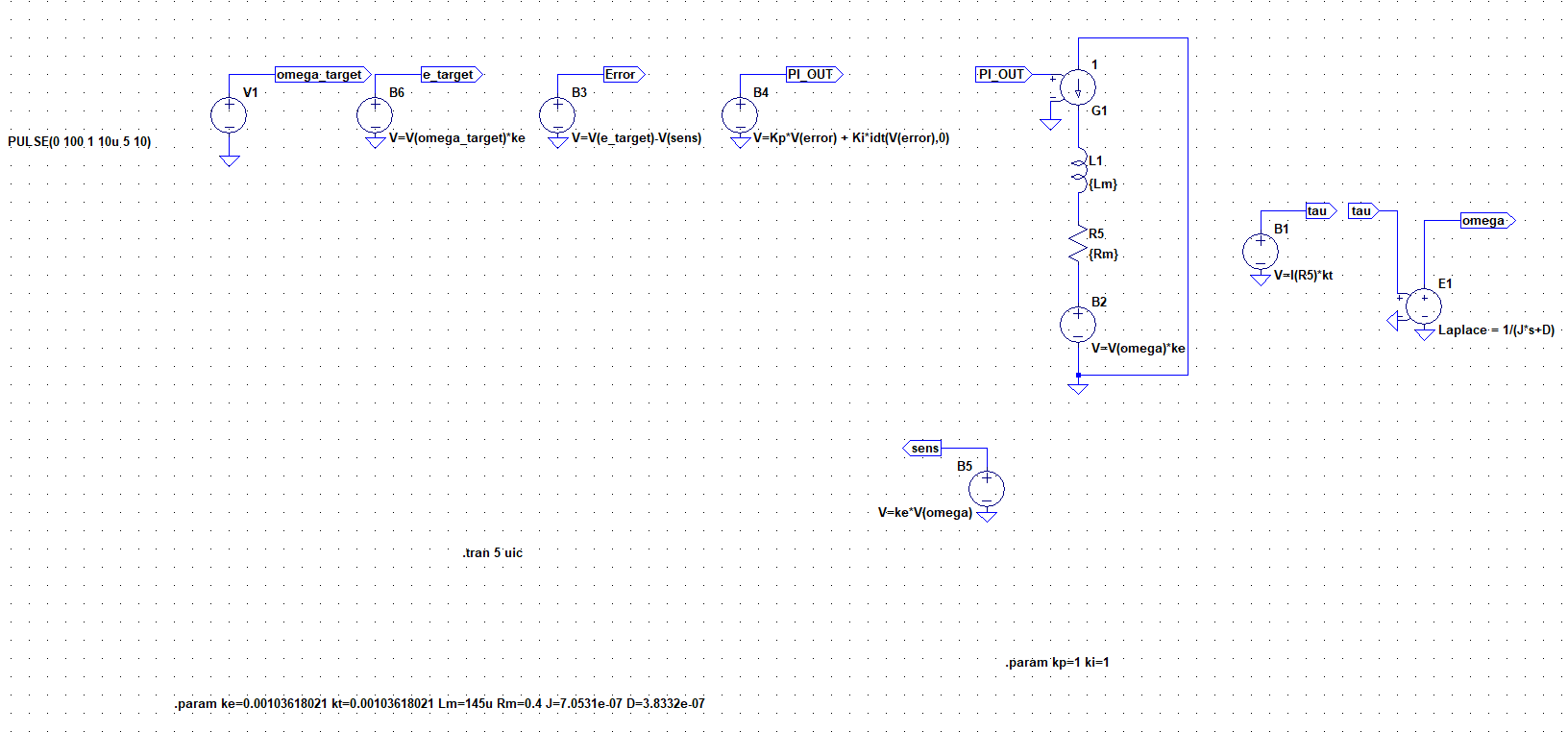
ステップ応答をシミュレーションすると
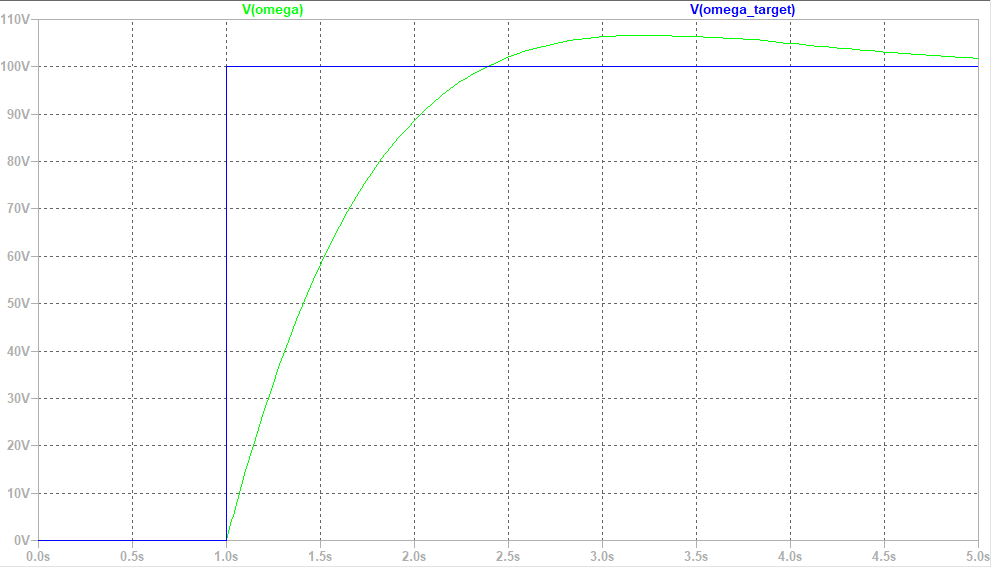
ゲイン調整の余地がありそうですがなんとなく動いています。
Kp=1,Ki=1で大きく外してはいないようなので、とりあえずこのまま進めましょう。
シミュレーションファイルはこちら
#回路への置き換え
それでは、これを少しずつ実際の電子部品を使った回路に置き換えていきましょう。
ブロックを一つ一つ置き換えるとこの図のような構成が考えられます。
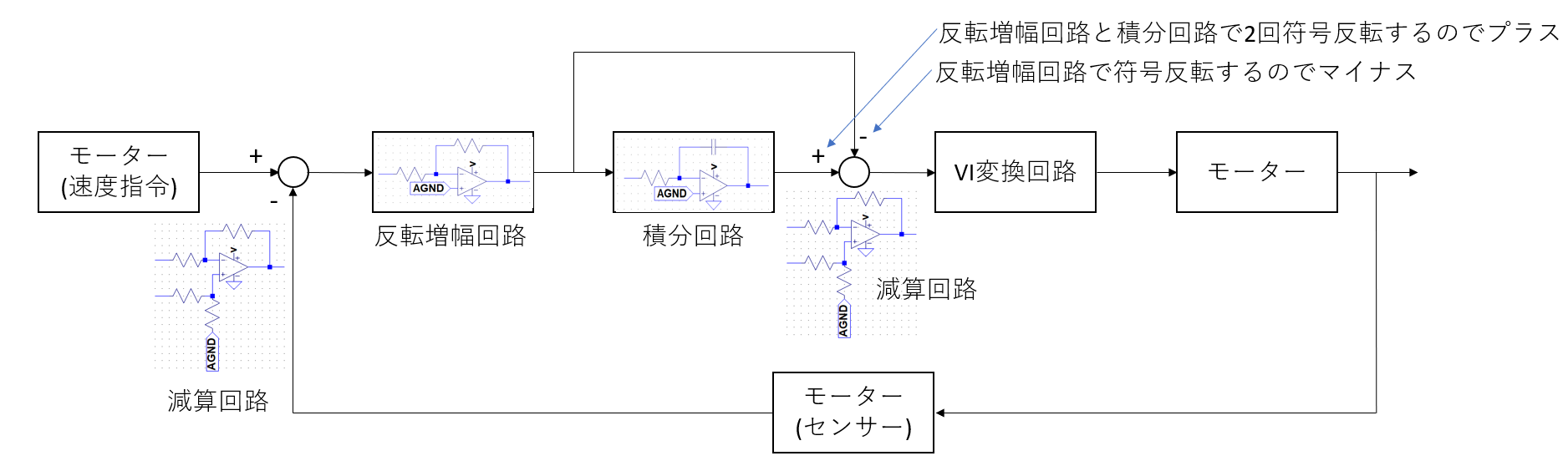
オペアンプが4個必要です。
作るのが少し面倒です。
そこで偏差を検出している減算回路にゲインを持たせられれば後段の反転増幅回路が不要になりそうです。
ここで問題になるのがゲイン調整の方法です。減算回路にゲインを持たせることはもちろん可能ですが、複数の抵抗値を同時に変えないとならないため半固定抵抗1個でゲイン調整するようなことができません。
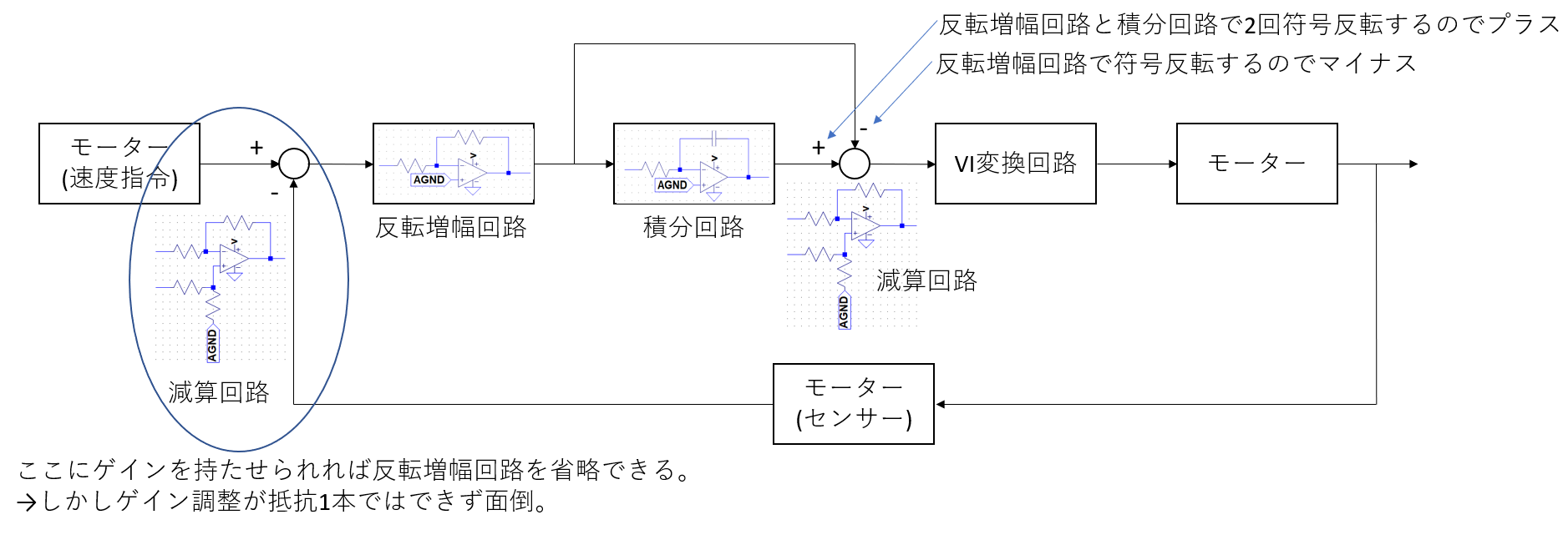
偏差の検出で本当に減算回路が必要でしょうか。
センサーとして使っているモーターの線を逆に接続していしまえば、信号の符号が反転しますからそうすれば加算回路で偏差が検出できることになります。
加算回路はフィードバック抵抗1本でゲインを調整することができるのでゲイン調整の問題はクリアになりました。
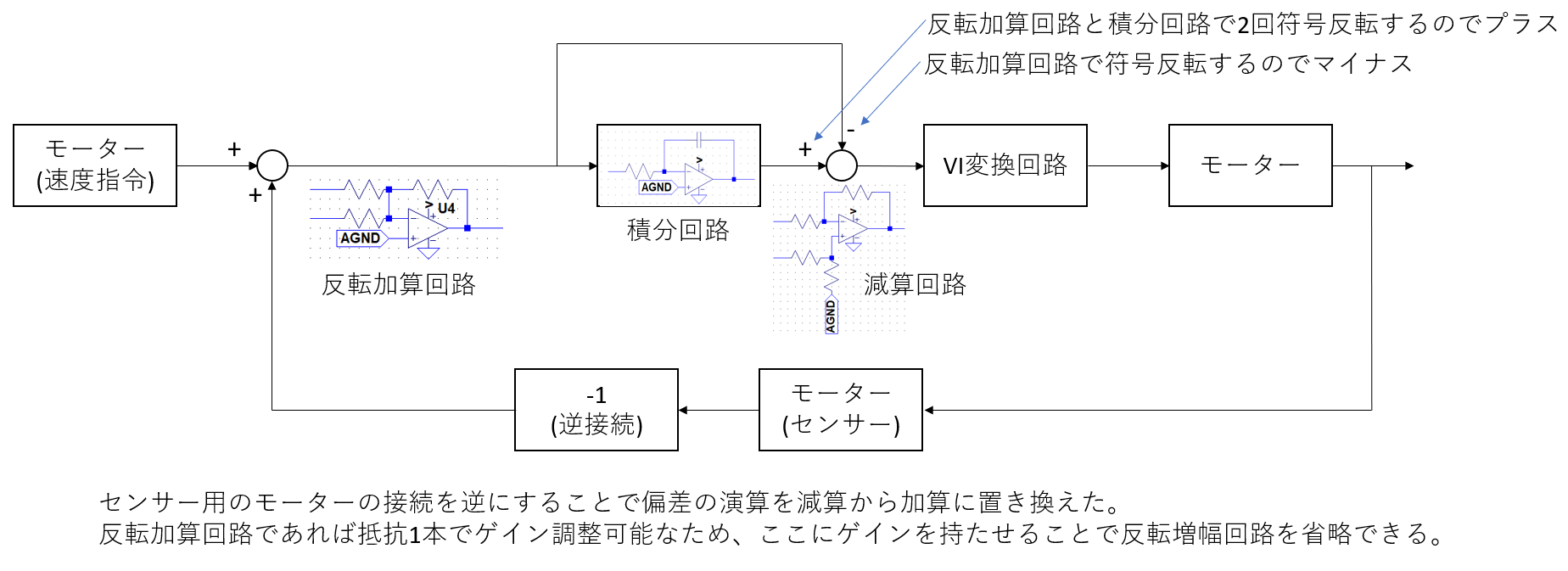
これでオペアンプ3個になりました。
VI変換回路前段の減算回路も本当に必要でしょうか。
VI変換回路がどういうものだったかというと
実は差動入力の回路でした。
つまりこれ自体が減算の機能を持っていると考えることができます。
減算回路は必要ありませんでした。
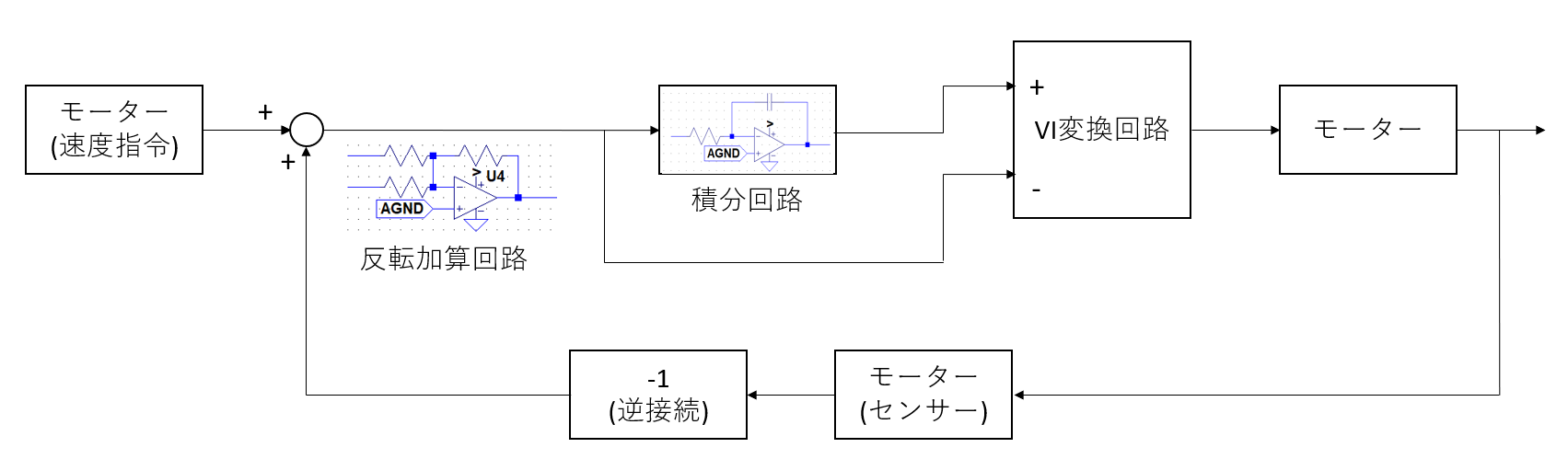
オペアンプ2個でPI制御が実現できることがわかりました。
このくらいだったら工作もそれほど大変ではないでしょう。
#VI変換回路の実装
まずはこの回路をLTspice上に作っていきます。
最初にVI変換回路を作ってみましょう。
電圧制御電流源でを使って表現していた部分をパワーオペアンプによるVI変換回路に置き換えました。
PI_OUTがGND基準ではなくAGND基準となっている点に注意してください。
C1とR11はモーターに流れる電流が急変した際にモーターのインダクタンス成分によって発生する起電力を吸収するスナバ回路です。
実際に回路を作成する時に必要になります。
シミュレーションしてみると
電圧制御電流源をVI変換回路に置き換えてもちゃんと制御できているようです。
シミュレーションファイルはこちら
#PI制御器の実装
ではPI制御器の部分も回路で置き換えていきましょう。
電源回路もついでに作ってしまいましょう。
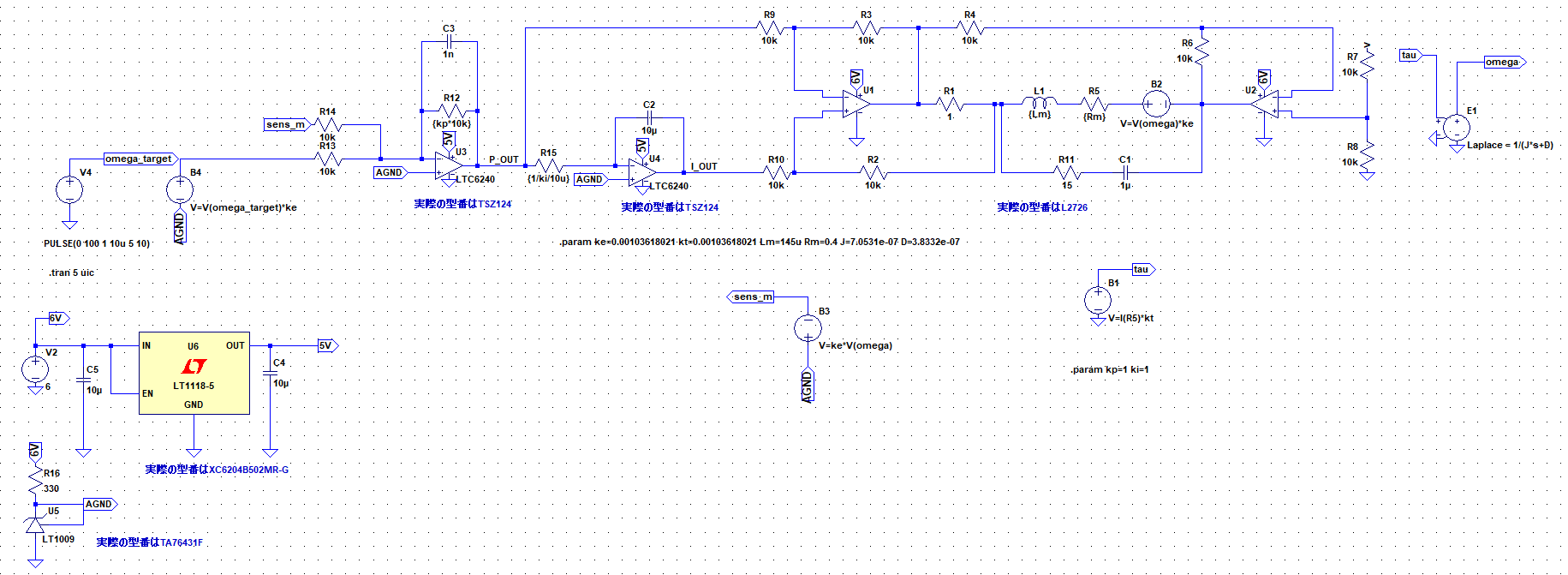
これで全てが回路になりました。
繰り返しになりますが、PI制御器はAGND基準で動いており、回転数などの物理変数はGND基準で動いているのでその点に注意してください。
反転加算回路のフィードバック抵抗の値は、入力抵抗をRinとすると
Kp*Rin
となります。
積分回路の入力抵抗の値は、コンデンサの値をCとすると
1/Ki/C
となります。
これをシミュレーションしてみると
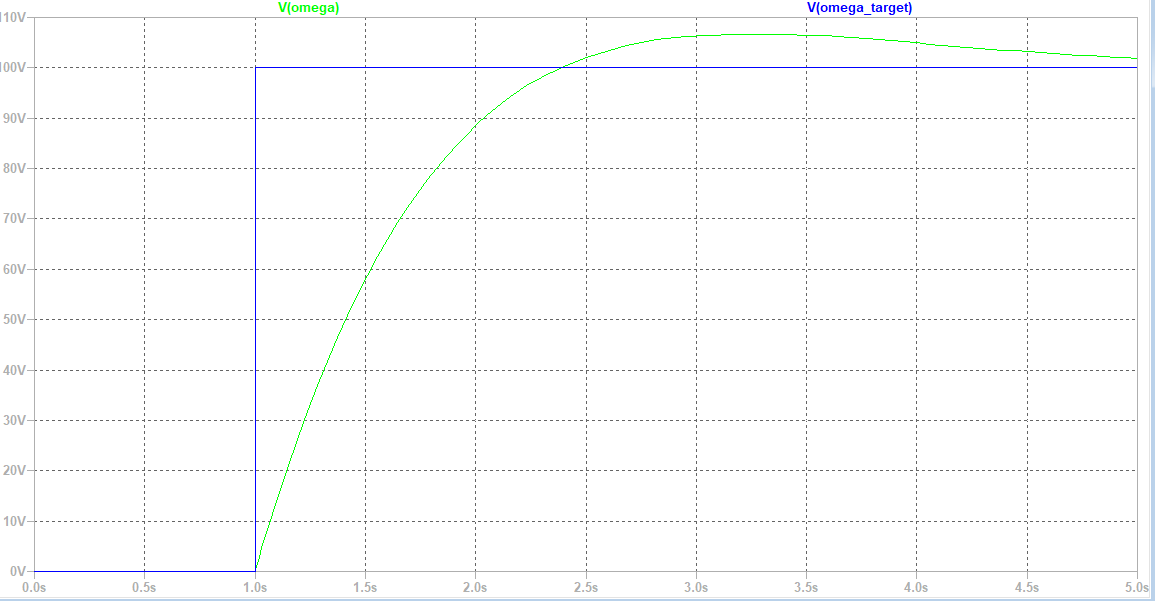
これも制御できています。
シミュレーションファイルはこちら
#実物の作成
シミュレーションで動作することがわかったので実際に回路を作ってみましょう。
ゲイン調整をする必要があるので、反転加算回路のフィードバック抵抗と積分回路の入力抵抗は500kΩの半固定抵抗を使います。
出力用のパワーオペアンプは、たまたま手持ちがあったL2726を使っています。
ディスコンなので追試する場合はL2720Wなど使った方が良いでしょう。
PI制御器にはTSZ124IPTを使っています。4回路入りを選んだ理由は、回路を作り始めた時点ではオペアンプ2個まで減らせることに気がついていなかったためです。
2回路入りで問題ありません。
2.5VのAGNDはシャントレギュレータのTA76431を使って作っています。…が、今回は4回路入りのオペアンプを使ったので5Vを1/2に分圧し、余っているオペアンプでボルテージフォロワしても良かったかもしれません。
これが作成した回路の全体写真です。

基板部分はこんな感じです。

工作が汚いのはご容赦ください…それと、実際には使うことがなかった減算回路が載ってます。
さて、実際に動かすとこんな感じになります。
Kp、Kiは現物で調整し、結果的にシミュレーションの時より大きくなっています。
右側のモーターが速度指令用で、左側のモーターが速度制御されたモーターです。
積分項により定常偏差を0にしようとする制御が働くので、このように非常に遅い速度指令を与えただけでもきちんと速度制御され速度指令に追従します。
本来高速で回すことを想定したモーターですが、速度制御を行うとここまでゆっくり動かすこともできるのです。
オペアンプ2個とパワーオペアンプ2個の非常に簡単な回路でPI制御が実現できるということがわかりました。
#PI制御をPID制御にしてみる
さて、今回の目的だとPID制御のP,I,DのうちPとIだけを使うPI制御で十分であると判断してDは入れませんでした。
しかし、入れてみたらどうなるのか気になるので余っているオペアンプで入れるだけ入れてみましょう。
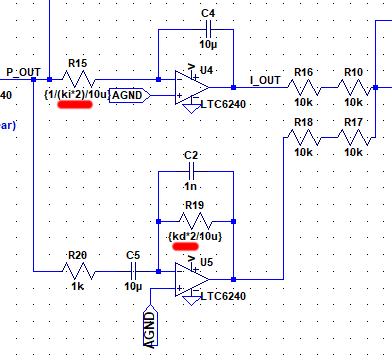
少々乱暴ではありますが、VI変換回路の入力抵抗部分でパッシブの加算器を構成し、積分回路と微分回路の出力の合成を行うことにしました。
この加算器によってゲインが1/2になってしまうので、それを補正するようにKiとKdを2倍にする必要があります。
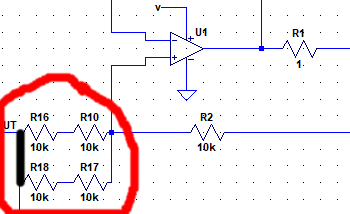
このように、後段の回路の入力抵抗を利用して信号の加算をする場合、並列合成抵抗(丸で囲った部分)の値がもともとの入力抵抗の値に等しくないと後段の回路の動作が変わってしまうので注意してください。
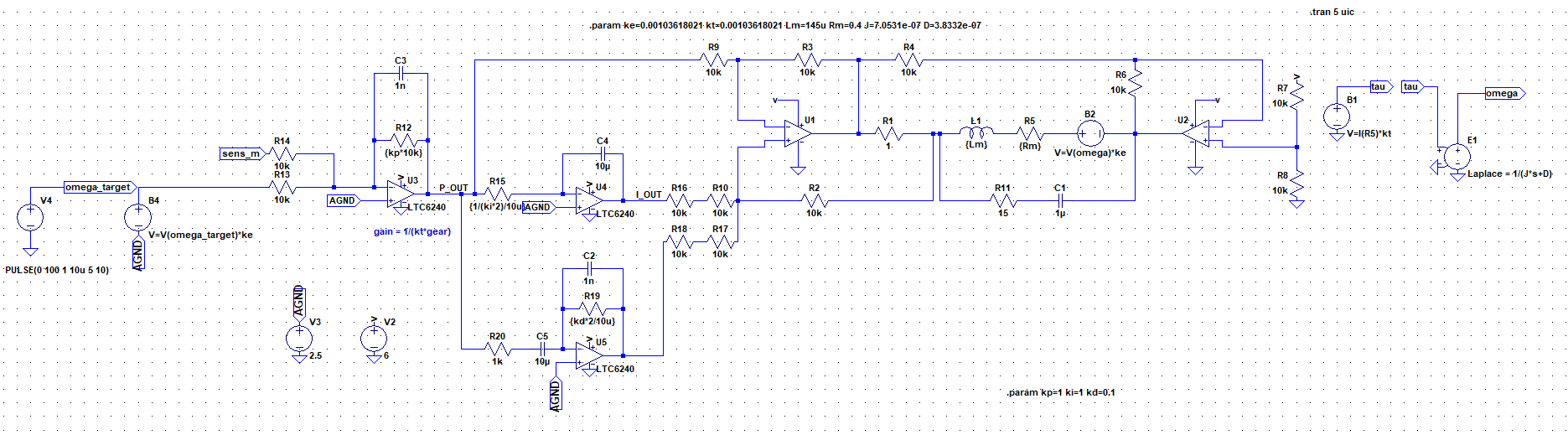
全体としてはこのようになります。
微分回路のフィードバック抵抗の決め方は、コンデンサの値をCとすると
Kd/C
となります。
今回の回路では、積分と微分の加算部分でゲインが1/2になるのでこれの2倍の値となります。
R20とC2は高い周波数でゲインが高くなりすぎないようにするためのもので、無いと発振します。
この値も制御対象によっては調整の必要があります。
さて、この微分回路を追加したものを実際に作ってみました。
その結果…
めっちゃ良く制御できるようになった!!
(冒頭の動画と同じです)
…と思いましたが、もしや、と思いKdを0にしても…全く動作が変わりません。
改造に伴ってKpとKiを再調整した結果制御性能が上がっただけで、微分の恩恵は特になかったようです。
PID制御の微分動作は、粘性摩擦に対して慣性モーメントの比が大きい系など、一度動き出したら止めにくいような系で効果を発揮します。
今回の系はモーター2個の軸同士をいい加減に接続していることもあり、とても摩擦の大きな系となっています。
このような系では、微分の恩恵があまりないのでしょう。
ともあれ、このオペアンプ3個のPID制御回路は今後何かをアナログ回路で制御したい場合にベースとすることができそうです。
最後までお読みいただきありがとうございます。
いかがだったでしょうか。
PID制御自体の解説やマイコンでの実装についてはwebにたくさんがありますので、あえてアナログ制御での解説をやってみました。
実際にこの設計を使うことは無いかもしれませんが、休日の息抜きとして楽しく執筆させていただきました。
#追記
12月4日に開催された、LTspiceユーザーの集い2018というイベントに行ってきました。
その中での株式会社モーデック 落合忠博氏による講演によると、LTspice用の制御モデルライブラリを同社で無料配布する予定ということです。
これを使うと、より簡単に本稿で扱ったようなモデルをシミュレーションできるはずです。
近日中に公開とのことなので、期待しましょう!
本記事は、Cerevoスタッフが業務や趣味について思うままに書き綴るアドベントカレンダー企画「Cerevo アドベントカレンダーTechBlog 2018」の第7日目です。
Cerevo アドベントカレンダーTechBlog 2018
http://tech-blog.cerevo.com/archives/category/adventcalendar/2018/
著者プロフィール
- Cerevo 電気エンジニア
最近の投稿
 11. その他2025.06.18書類提出のみで工事設計認証を取得した話
11. その他2025.06.18書類提出のみで工事設計認証を取得した話 04. 電気設計2025.05.28秋月製無線給電モジュールの高性能化改造
04. 電気設計2025.05.28秋月製無線給電モジュールの高性能化改造 04. 電気設計2025.05.13認証不要の小型無線給電モジュールを試す
04. 電気設計2025.05.13認証不要の小型無線給電モジュールを試す 05. 実験・比較2021.12.10中華ログペリアンテナを120%活かした社内EMC試験の方法 – アンテナファクタ付で販売も
05. 実験・比較2021.12.10中華ログペリアンテナを120%活かした社内EMC試験の方法 – アンテナファクタ付で販売も